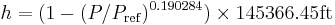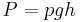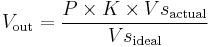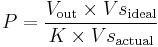Pressure sensor

A pressure sensor measures pressure, typically of gases or liquids. Pressure is an expression of the force required to stop a fluid from expanding, and is usually stated in terms of force per unit area. A pressure sensor usually acts as a transducer; it generates a signal as a function of the pressure imposed. For the purposes of this article, such a signal is electrical.

Pressure sensors are used for control and monitoring in thousands of everyday applications. Pressure sensors can also be used to indirectly measure other variables such as fluid/gas flow, speed, water level, and altitude. Pressure sensors can alternatively be called pressure transducers, pressure transmitters, pressure senders, pressure indicators and piezometers, manometers, among other names.

Pressure sensors can vary drastically in technology, design, performance, application suitability and cost. A conservative estimate would be that there may be over 50 technologies and at least 300 companies making pressure sensors worldwide.

There is also a category of pressure sensors that are designed to measure in a dynamic mode for capturing very high speed changes in pressure. Example applications for this type of sensor would be in the measuring of combustion pressure in an engine cylinder or in a gas turbine. These sensors are commonly manufactured out of piezoelectric materials such as quartz.

Some pressure sensors, such as those found in some traffic enforcement cameras, function in a binary (on/off) manner, i.e., when pressure is applied to a pressure sensor, the sensor acts to complete or break an electrical circuit. These types of sensors are also known as a pressure switch.

Contents

Types of pressure measurements

Pressure sensors can be classified in terms of pressure ranges they measure, temperature ranges of operation, and most importantly the type of pressure they measure. In terms of pressure type, pressure sensors can be divided into five categories:

This sensor measures the pressure relative to perfect vacuum pressure (0 PSI or no pressure). Atmospheric pressure is 101.325 kPa (14.7 PSI) at sea level with reference to vacuum.

This sensor is used in different applications because it can be calibrated to measure the pressure relative to a given atmospheric pressure at a given location. A tire pressure gauge is an example of gauge pressure indication. When the tire pressure gauge reads 0 PSI, there is really 14.7 PSI (atmospheric pressure) in the tire.

This sensor is used to measure pressure less than the atmospheric pressure at a given location. This has the potential to cause some confusion as industry may refer to a vacuum sensor as one which is referenced to either atmospheric pressure (i.e. measure Negative gauge pressure) or relative to absolute vacuum.

This sensor measures the difference between two or more pressures introduced as inputs to the sensing unit, for example, measuring the pressure drop across an oil filter. Differential pressure is also used to measure flow or level in pressurized vessels.

This sensor is the same as the gauge pressure sensor except that it is previously calibrated by manufacturers to measure pressure relative to sea level pressure.

Pressure-sensing technology

There are two basic categories of analog pressure sensors.

Force collector types These types of electronic pressure sensors generally use a force collector (such a diaphragm, piston, bourdon tube, or bellows) to measure strain (or deflection) due to applied force (pressure) over an area.

Uses the piezoresistive effect of bonded or formed strain gauges to detect strain due to applied pressure. Common technology types are Silicon (Monocrystalline), Polysilicon Thin Film, Bonded Metal Foil, Thick Film, and Sputtered Thin Film. Generally, the strain gauges are connected to form a Wheatstone bridge circuit to maximize the output of the sensor. This is the most commonly employed sensing technology for general purpose pressure measurement. Generally, these technologies are suited to measure absolute, gauge, vacuum, and differential pressures.
Uses a diaphragm and pressure cavity to create a variable capacitor to detect strain due to applied pressure. Common technologies use metal, ceramic, and silicon diaphragms. Generally, these technologies are most applied to low pressures (Absolute, Differential and Gauge)
Measures the displacement of a diaphragm by means of changes in inductance (reluctance), LVDT, Hall Effect, or by eddy current principle.
Uses the piezoelectric effect in certain materials such as quartz to measure the strain upon the sensing mechanism due to pressure. This technology is commonly employed for the measurement of highly dynamic pressures.
Techniques include the use of the physical change of an optical fiber to detect strain due to applied pressure. A common example of this type utilizes Fiber Bragg Gratings. This technology is employed in challenging applications where the measurement may be highly remote, under high temperature, or may benefit from technologies inherently immune to electromagnetic interference. Another analogous technique utilizes an elastic film constructed in layers that can change reflected wavelengths according to the applied pressure (strain).[1].
Uses the motion of a wiper along a resistive mechanism to detect the strain caused by applied pressure.

Other types

These types of electronic pressure sensors use other properties (such as density) to infer pressure of a gas, or liquid.

Uses the changes in resonant frequency in a sensing mechanism to measure stress, or changes in gas density, caused by applied pressure. This technology may be used in conjunction with a force collector, such as those in the category above. Alternatively, resonant technology may be employed by expose the resonating element itself to the media, whereby the resonant frequency is dependent upon the density of the media. Sensors have been made out of vibrating wire, vibrating cylinders, quartz, and silicon MEMS. Generally, this technology is considered to provide very stable readings over time.
Uses the changes in thermal conductivity of a gas due to density changes to measure pressure. A common example of this type is the Pirani gauge.
Measures the flow of charged gas particles (ions) which varies due to density changes to measure pressure. Common examples are the Hot and Cold Cathode gages.
There are numerous other ways to derive pressure from its density (speed of sound, mass, index of refraction) among others.

Applications

There are many applications for pressure sensors:

This is where the measurement of interest is pressure, expressed as a force per unit area (. This is useful in weather instrumentation, aircraft, automobiles, and any other machinery that has pressure functionality implemented.

This is useful in aircraft, rockets, satellites, weather balloons, and many other applications. All these applications make use of the relationship between changes in pressure relative to the altitude. This relationship is governed by the following equation[2]:

h = (1-(P/P_\mathrm{ref})^{0.190284}) \times 145366.45\mathrm{ ft}

This equation is calibrated for an altimeter, up to 36,090 feet (11,000 m). Outside that range, an error will be introduced which can be calculated differently for each different pressure sensor. These error calculations will factor in the error introduced by the change in temperature as we go up.

Barometric pressure sensors can have an altitude resolution of less than 1 meter, which is significantly better than GPS systems (about 20 meters altitude resolution). In navigation applications altimeters are used to distinguish between stacked road levels for car navigation and floor levels in buildings for pedestrian navigation.

This is the use of pressure sensors in conjunction with the venturi effect to measure flow. Differential pressure is measured between two segments of a venturi tube that have a different aperture. The pressure difference between the two segments is directly proportional to the flow rate through the venturi tube. A low pressure sensor is almost always required as the pressure difference is relatively small.

A pressure sensor may also be used to calculate the level of a fluid. This technique is commonly employed to measure the depth of a submerged body (such as a diver or submarine), or level of contents in a tank (such as in a water tower). For most practical purposes, fluid level is directly proportional to pressure. In the case of fresh water where the contents are under atmospheric pressure, 1psi = 27.7 inH20 / 1Pa = 9.81 mmH20. The basic equation for such a measurement is

P = pgh \,

where P = pressure, p = density of the fluid, g = standard gravity, h = height of fluid column above pressure sensor

A pressure sensor may be used to sense the decay of pressure due to a system leak. This is commonly done by either comparison to a known leak using differential pressure, or by means of utilizing the pressure sensor to measure pressure change over time.

Piezoresistive transducers configured as Wheatstone bridges often exhibit ratiometric behavior with respect not only to the measured pressure, but also the transducer supply voltage.

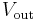V_\mathrm{out} ={ P \times K \times Vs_\mathrm{actual} \over Vs_\mathrm{ideal} }

where:

V_\mathrm{out} is the output voltage of the transducer.

P is the actual measured pressure.

K is the nominal transducer scale factor (given an ideal transducer supply voltage) in units of voltage per pressure.

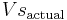Vs_\mathrm{actual} is the actual transducer supply voltage.

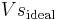Vs_\mathrm{ideal} is the ideal transducer supply voltage.

Correcting measurements from transducers exhibiting this behavior requires measuring the actual transducer supply voltage as well as the output voltage and applying the inverse transform of this behavior to the output signal:

P = {V_\mathrm{out} \times Vs_\mathrm{ideal} \over K \times Vs_\mathrm{actual} }

NOTE: Common mode signals often present in transducers configured as Wheatstone bridges are not considered in this analysis.

See also

References

  1. ^ Elastic hologram' pages 113-117, Proc. of the IGC 2010, ISBN 978-0-9566139-1-2 here: http://www.dspace.cam.ac.uk/handle/1810/225960
  2. ^ http://www.wrh.noaa.gov/slc/projects/wxcalc/formulas/pressureAltitude.pdf National Oceanic and Atmospheric Association